TIGA EKOR AYAM + TUJUH EKOR ITIK = 10 EKOR ANGSA?

Anda akan ketawa apabila melihat persamaan di atas. Tidak masuk akal. Dari sudut sains, unitnya sahaja tidak sama. Ibarat 3 kg + 4°C = 10 m. Kita tinggalkan sebentar kisah ayam, itik dan angsa tersebut. Sekarang kita cuba lihat satu istilah sains, iaitu Kehomogenan Dimensi (Dimensional Homogeneity).

Kehomogenan Dimensi

Kehomogenan Dimensi adalah istilah merujuk pada persamaan yang mana unit di sebelah kanan dan di sebelah kiri adalah sama. Sebagai contoh mari kita lihat persamaan yang biasa kita lihat, iaitu persamaan gerakan linear.

Sepertimana yang diketahui, ‘v’ di sini merujuk pada halaju sebelum dan ‘u’ merujuk halaju selepas di dalam unit m/s. Manakala, ‘a’ merupakan pecutan di dalam unit m/s² dan ‘s’ adalah sesaran di dalam unit m.

Terbukti persamaan di atas termasuk di dalam kategori persamaan yang Dimensinya homogen. Iaitu kuasa meter dan saat di sebelah kanan sama dengan sebelah kiri. Dan ya, anda boleh pergi jauh dengan melihat pelbagai persamaan lain seperti persamaan yang biasa kita lihat, Hukum Newton kedua, persamaan Bernoulli atau persamaan yang lebih rumit, persamaan Navier-Stokes. Kesemuanya persamaan ini mematuhi konsep Kehomogenan Dimensi.

Tetapi tahukah anda ada beberapa persamaan di bidang kejuruteraan yang konsepnya seperti ayam, itik dan angsa tadi? Dalam erti kata lain persamaan yang tidak mematuhi Kehomogenan Dimensi.

Konsep Ayam, Itik dan Angsa

Sebagai contoh persamaan Hazen-William. Persamaan ini digunakan untuk mengira perbezaan tekanan dalam paip air. Persamaan ini diberikan oleh,

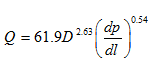
Di mana Q merupakan kadar alir di dalam m³/s, D adalah diameter paip, dp/dl adalah perbezaan tekanan per unit panjang. Tanpa perlu melihat jauh, disebabkan terdapat kuasa ‘pelik’ iaitu 2.63 dan 0.54, dapat diketahui persamaan ini tidak homogen dari segi dimensi.

Jadi persamaan ini salah. Mungkin itu yang terlintas di fikiran anda. Sebelum kita membuat kesimpulan, kita lihat satu lagi contoh persamaan lain, persamaan Manning. Persamaan ini digunakan untuk mencari halaju air bagi sistem aliran saluran terbuka (Open channel flow).

Di mana C merupakan pemalar rintangan aliran, R adalah jejari di dalam meter, dan S adalah kecerunan saluran (tiada unit). Manning membentangkan hasil kajiannya pada tahun 1889. Persamaan Manning ini hampir sama dengan apa yang telah dikemukakan oleh Gauckler pada 1868. Disebabkan hal ini terkadang persamaan ini juga dikenali dengan Persamaan Gauckler-Manning. Terdapat beberapa analisis penting terhadap persamaan ini dilakukan oleh Strickler pada 1923. Oleh yang demikian di Eropah persamaan ini lebih dikenali dengan Persamaan Gauckler-Manning- Strickler.

Sekarang mari kita lihat bentuk yang paling kerap digunakan untuk menggambarkan persamaan Manning ini. Di mana C di tukar kepada 1/n atau kepada K menurut Strickler.

Persamaan di atas ini adalah persamaan yang pelik. Ini kerana untuk menjadikan ia sebagai persamaan yang mematuhi konsep kehomogenan dimensi, pemalar n perlu mempunyai unit s/m^1/3. Sedangkan n adalah pemalar tanpa unit seperti mana tercatat dalam buku dan jurnal. Jika diterima n dengan unit yang demikian, ianya juga susah untuk dihadam kerana unitnya yang agak pelik.

Katakanlah pemalar n ini mempunyai unit s/m^1/3, jadi apabila persamaan di atas digunakan untuk mengira halaju aliran mengikut sistem Imperial, iaitu halaju di dalam unit kaki/saat (ft/s), sepatutnya nilai n ini ditukar kepada s/ft^1/3. Namun ini amatlah menyukarkan kerana nilai n perlu ditukar untuk setiap kali pengiraan.

Terdapat pula cadangan bahawa unit s/m^1/3 ini bukanlah untuk n, tetapi untuk nilai 1 di dalam persamaan tersebut. Inilah cadangan yang kelihatan terbaik meskipun masih membingungkan kerana 1 hanyalah nombor dan bukan sebarang parameter. Terdapat pelbagai cara lain turut dikemukakan namun, hakikatnya ianya tidak menutup kecacatan yang ada pada persamaan ini.

.

Jadi berbalik kepada isu asal, adakah persamaan-persamaan ini salah? Secara matematiknya boleh dikatakan salah, tetapi hakikatnya persamaan ini tidaklah salah secara keseluruhan. Apatah lagi persamaan-persamaan ini telah menunjukkan keputusan yang baik.

Persamaan Hazen-William misalnya, digunakan secara meluas di dalam reka bentuk sistem perpaipan seperti sistem pemercik (fire sprinkler systems), sistem pengagihan air (water supply networks)  dan sistem pengairan (irrigation systems). Manakala persamaan Manning pulasangat popular digunakan untuk permasalahan sistem aliran terbuka.

Persamaan-persamaan ini lebih dikenali dengan istilah persamaan empirikal, di mana ianya dihasilkan dengan membandingkan data-data uji kaji. Sebagai contoh, Manning telah menghasilkan persamaan tersebut dengan membandingkan data-data dari 170 uji kaji yang telah dilakukan.

Maka secara ringkasnya persamaan-persamaan ini hendaklah digunakan dengan berhati-hati dengan mengambil kira kekangan yang telah di nyatakan. Sebagai contoh Persamaan Hazen-William hanya boleh digunakan untuk air sahaja. Ia juga tidak mengambil kira kesan suhu dan kelikatan air tersebut.

Jadi adakah TIGA EKOR AYAM + TUJUH EKOR ITIK = 10 EKOR ANGSA itu benar? Jawapannya tidak. Kerana tiada data dari hasil uji kaji menyatakan sedemikian, kecuali jika para pembaca dapat membuktikannya.

Disediakan oleh,

Nurudin Abdul Settar

Pensyarah Bidang Kejuruteraan.

RUJUKAN

[1]         P. J. Pritchard, Fox and McDonald’s Introduction to Fluid Mechanics, 8th edition. John Wiley & Sons, 2010.

[2]         J. F. Douglas, J. M. Gasiorek, J. A. Swaffield, and L. B. Jack, Fluid Mechanics, 5th ed. Pearson/Prentice Hall, 2005.

[3]         F. M. White, Fluid Mechanics, 7th ed. McGraw Hill, 2011.

[4]         V. Te Chow, Open-channel Hydraulics. Blackburn Press, 1959.

[5]         W. H. Hager, “Gauckler and the GMS Formula,” J. Hydraul. Eng., vol. 127, no. 8, pp. 635–638, Aug. 2001.

[6]         W. H. Hager, “Albert strickler: His life and work,” J. Hydraul. Eng., vol. 141, no. 7, pp. 1–5, 2015.