Tahukah anda, pembinaan konsep operasi asas aritmetik bermula pada kurun ke-9 oleh Al-Khawarizmi. Beliau telah menulis sekurang-kurangnya dua judul buku untuk menerangkan operasi asas ini, iaitu Kitab al-Jam’ wa al-Tafriq dan Hisab al-Hind.
Menurut huraian Algoritmi de numero Indorum yang dipercayai terjemahan Kitab al-Jam’ wa al-Tafriq dalam Bahasa Latin, operasi ini melibatkan penambahan, penolakan, pembahagian dua, gandaan dua, pendaraban dan pembahagian. Permulaan penggunaan konsep ini adalah menggunakan penulisan nombor dalam sistem sepuluh dengan pendekatan operasi polinomial.
OPERASI POLINOMIAL PENDEKATAN OPERASI ASAS ARITMETIK
Penambahan dua integer bermaksud penambahan dua polinomial.

Begitu juga dengan operasi penolakan, pendaraban dan pembahagian, menggunakan konsep yang sama. Contohnya, teknik pendaraban antara 123 dan 24 dilakukan dengan pendaraban polinomial,
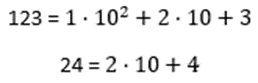

Kemudian, pada kurun ke-14, Jamshid al-Kasyi telah memperkenalkan satu kaedah pendaraban yang mengabaikan semua monomial, dan hanya menuliskan pekali polinomial.

Kaedah ini menjadi paling popular dalam tamadun Islam, dan seterusnya menjadi popular di Eropah setelah matematik Islam diperkenalkan ke benua itu. Kaedah ini jugalah yang dikembangkan sehingga ke era ini.
PENAMBAHAN
Bagi menerangkan perihal operasi penambahan, al-Uqlidisi memberikan contoh penambahan 3426 terhadap 19857, yang mana nombor kecil biasanya ditambah kepada nombor yang lebih besar.

Al-Uqlidisi menerangkan kaedah ini seperti berikut :
‘Kita memulakan penambahan 3 kepada 9; 3 dan 9 ialah 12, kita masukkan 2 di tempat 9 dan tambahkan 10 terhadap 1 lalu terhasilkan 2. Kita tambahkan 4 kepada 8, 2 kepada 5 dan 6 terhadap 7. Hasilnya ialah 23283.’
Nombor pertama disebut sebagai al-mazid ‘alaihi (nombor yang ditambah ke atasnya) dan nombor kedua disebut sebagai al-mazid (nombor yang ditambah). Mengikut penerangan Al-Uqlidisi, proses penambahan dilakukan dari kiri ke kanan.
Proses ini kemudiannya terus ditambahbaik oleh ilmuwan-ilmuwan Islam yang lain, seperti Kusyar (kurun 11M) dan Nasir al-Din al-Tusi (kurun 12M) sehinggalah perkembangan seterusnya memperlihatkan proses penambahan yang dimulakan dari kanan ke kiri lebih terkenal kerana prosesnya lebih ringkas. Penambahan kanan ke kiri ini telah dicatatkan oleh Al-Uqlidisi dalam karyanya, al-Fusul.
PENOLAKAN
Konsep penolakan melibatkan nombor kecil yang ditolak daripada nombor yang besar. Jika martabat nombor tertentu digit nombor yang kecil lebih besar, maka, konsep peminjaman daripada martabat yang lebih tinggi dilakukan. Al-Uqlidisi cuba menerangkan kaedah ini untuk penolakan 3457 daripada 5746 seperti berikut :
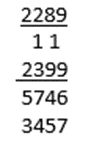
‘Kita mulakan dengan menolak 3 daripada 5, tempat 5 tinggal 2; kita tolak 4 daripada 7, tempat 7 tinggal 3; kita ingin menolak 5 daripada 4 tetapi ini tidak mencukupi; 5 lebih besar daripada 4, kita pinjam 1 daripada nombor selepas 4, di situ kita dapati 3 dan di tempat 3 tinggal 2. Nilai 1 tadi ialah 10 berbanding dengan 4; 10 tolak 4 dan masukkan hasil ini di tempat 4 maka tempat 4 menjadi 9; kemudian kita mahu tolak 7 daripada 6; ulang proses tadi, ambil 1 daripada 9 yang merupakan 10 berbanding terhadap 6 dan ditolak 7 dan tambahkan baki 10 kepada 6, terhasillah 9 di tempat 6.’
Fuh! Pinar mata baca.
Perkembangan kaedah ini juga membawa kepada penemuan penolakan kanan ke kiri yang lebih mudah dan digunakan oleh ahli matematik mutakhir.
PENDARABAN
Kaedah ini melibatkan penambahan sesuatu nombor dengan dirinya sendiri beberapa kali. Sebelum memulakan operasi ini, al-Uqlidisi dan al-Tusi menyarankan para pelajarnya menghafal sifir pendaraban nombor 1 hingga 9 seperti yang ditunjukkan dalam rajah di bawah.

Kemudian, proses pendaraban dikembangkan kepada beberapa cara yang semuanya digunakan sehingga kini. Antaranya, pendaraban melibatkan nombor perpuluhan, pendaraban puluhan dengan puluhan, pendaraban melibatkan sifar, pendaraban ratusan dengan ratusan, pendaraban cara menegak dan pendaraban cara kotak.
Kaedah ‘Lattice’ ataupun kaedah kekisi yang digunakan dalam silibus sekolah rendah sekarang juga telah diperkenalkan dan disebut sebagai kaedah jaringan oleh ilmuwan Islam. Kaedah ini menjadi popular selepas kurun ke-13M dan digunakan oleh al-Kasyi di dalam karyanya, Miftah al-Hisab dan al-‘Amili di dalam Khulasah al-Hisab.

Kemudian, kaedah ini dikembangkan lagi sehinggalah mencapai tahap kaedah yang diterima umum sepertimana kaedah lazim yang kita gunakan sekarang.
PEMBAHAGIAN
Proses pembahagian ditakrifkan oleh al-Tusi sebagai proses yang bersetentangan dengan pendaraban.
Proses ini merupakan proses yang sangat sukar kerana melibatkan salingan polinomial. Kemudian, al-Khawarizmi cuba untuk memudahkan lagi pekali polinomial yang terlibat, yang akhirnya al-Khawarizmi menemui satu kaedah pembahagian yang bersistem, dan telah diguna sehingga ke hari ini. Kaedah ini ditunjukkan dalam rajah dibawah.

KESIMPULAN
Daripada penemuan-penemuan ini, jelaslah kepada kita bagaimana al-Khawarizmi dan pengikut-pengikutnya menempa sejarah dunia dalam memainkan peranan penting memudahkan konsep asas ilmu matematik yang digunakan sehingga ke zaman kini.
Rujukan :
- Buku ‘Matematik Merentas Tamadun’, Mat Rofa Ismail.
- Buku ‘Sejarah Aritmetik dan Al-Jabar Islam’, Mat Rofa Ismail.










